
"An equation is a work of art if it is simple, can be solved exactly in terms of well-known functions, gives rise to a picture, is filled with information, has an expression of symmetry, and teaches us something new."
Magazine
Winter/Spring 2002
A
pursuit of beauty
by Paul McKinney ’52
The equation of motion for particle systems, especially in the world
of atoms and molecules, is a pursuit of beauty—quantum mechanics,
it is called. An equation is a work of art if it is simple, can be solved
exactly in terms of well-known functions, gives rise to a picture, is
filled with information, has an expression of symmetry, and teaches us
something new. Here is an example of one of my recent quantum reveries:
Suppose you have two deltons, my name for some as yet unknown and undiscovered
particles, moving on a straight wire of length L. Usually the deltons
ignore each other, are unaware of each other’s existence; however,
if they occupy the same position, they repel each other infinitely.
Erwin Schrödinger showed us how to find the probability density functions
and the energies for such wave-particle systems in the 1930s. A probability
density function is like a photograph—a snapshot of the deltons if
we take their picture over and over again. For this system, it is not
possible to separate out the motion of each individual delton, but, interestingly
enough, I can solve the equation exactly for the two particle system using
well-known trigonometry functions, sines, and applying the system’s
boundary conditions, I calculate an infinite set of discrete energy levels.
Mathematica, a computer program which transforms equations into beautiful
pictures, can plot two different views of probability density functions:
Three-dimensional graphs and contour maps. Selecting just one energy level,
I discover two probability density functions—I only expected one!
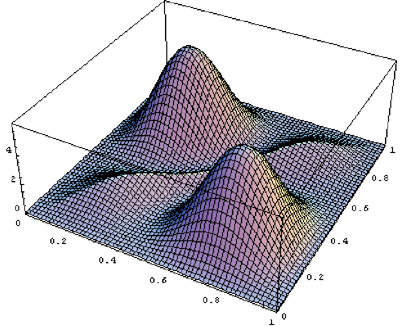
Look: the graph has four elements of symmetry! The identity, two planes
of reflection along the diagonals of the square, and a 180 degree axis
of rotation about the center of the square. The hills on the 3-D graphs
tell the most probable places to find the deltons. Even though the deltons
repel each other infinitely when they are at the same position, there
is a finite probability that they will occupy the same position according
to the graphs. Strange, but exciting!
Now the door to the problem’s information is open! My curiosity is
piqued! A feeling of pleasure grips me! The initial result’s beauty
stimulates me to explore the problem’s landscape further!
Paul McKinney is professor of chemistry and dean emeritus at Wabash.
Return to the table of contents
